Maschenstromverfahren
Maschenstromverfahren
Theorie
Teilschritte
Jedes elektrische Netzwerk kann durch ein lineares Gleichungssystem (im stationären Zustand mit linearen Bauelementen) oder durch ein Differentialgleichungssystem (bei in-stationären Vorgängen mit Kondensatoren und Induktivitäten) beschrieben und berechnet werden.
Bei dieser Methode werden nur Maschengleichungen für die sogenannten Maschenströme aufgestellt. Unter den Maschenströmen IM1 und IM2 usw. versteht man gedachte (fiktive) Kreisströme, die in den einzelnen Maschen fließend die gleich Wirkung (z.B. gleiche Spannungsabfälle) ergeben wie die tatsächlichen in den einzelnen Widerständen fließenden Ströme I1, I2 usw.
- Umwandlung in Spannungsquellen Alle realen Stromquellen müssen als ersten Schritt in reale Spannungsquellen umgewandelt werden.
- Maschen definieren Finde die Maschen im elektrischen Netzwerk. In jeder Masche fließt kreisförmig ein zugehöriger Maschenstrom. Zeichne die Richtung der Maschenströme ein.
- Aufstellen der Maschengleichungen Die Maschengleichungen werden mithilfe der Kreisströme aufgestellt. Es müssen unabhängige Gleichungen entstehen. Es müssen gleich viele Gleichungen und Unbekannte entstehen.
- Gleichungen nach Maschenströmen auflösen Aus den Maschengleichungen können über Einsetzverfahren, Eliminationsverfahren, oder ähnliche die Maschenströme berechnet werden.
- Gesuchte Größen berechnen Die gesuchten Spannungen und Ströme können mithilfe der Maschenströme berechnet werden.
Video Erklärung
Beispiel
Einführungsbeispiel
Gegeben ist folgendes Beispiel
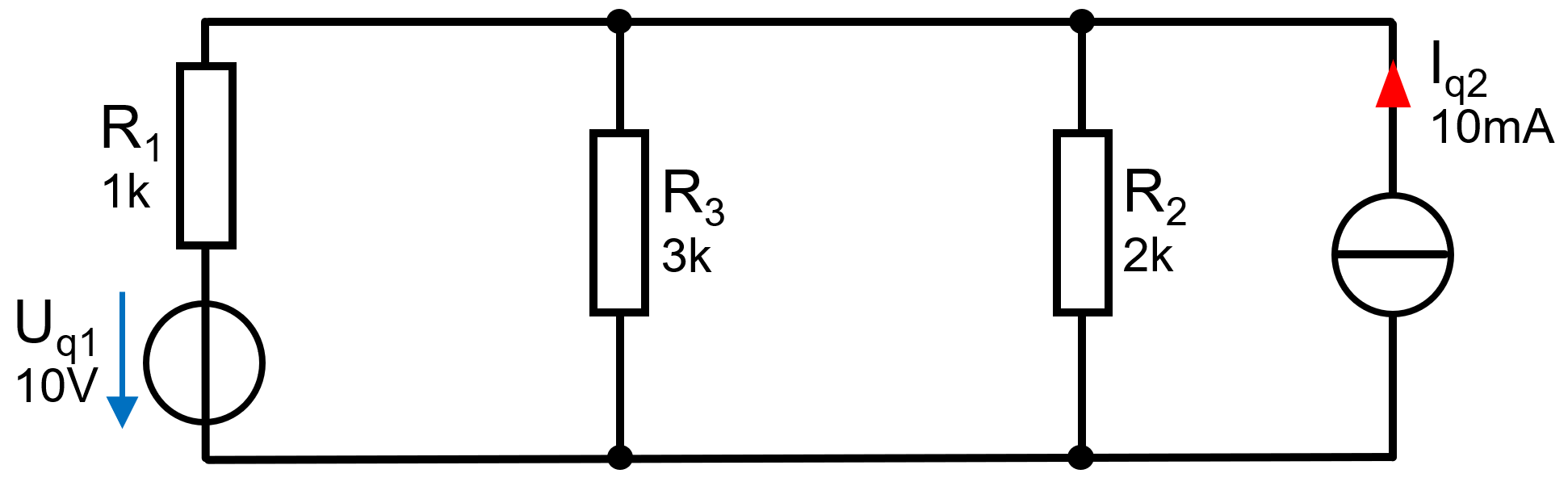
Angabe
Lösung
-
Umwandlung in Spannungsquellen: Da wie im Teil Theorie beschrieben, das Maschenstromverfahren ausschließlich Spannungsquellen verlangt, muss die Stromquelle zu einer Spannungsquelle gewandelt werden.
Die Quellenspannung der realen Spannungsquelle kann aus der Stromquelle mit Uq2 = Iq2 \cdot R2 = 1mA \cdot 2kOhm = 2V. Zu bedenken ist, dass der Innenwiderstand der realen Stromquelle den selben Wert annimmt wie die der Spannungsquelle. Der Unterschied liegt in der Position des Widerstandes. Somit ergibt sich folgende Schaltung: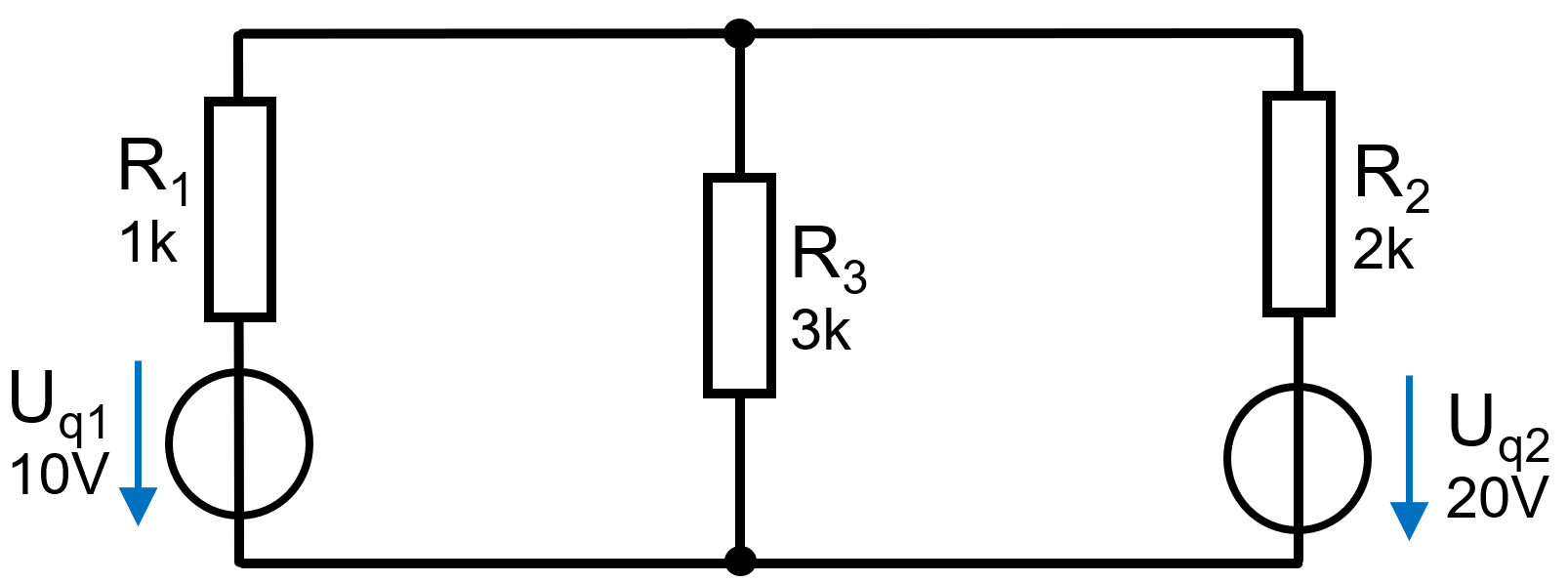
Reale Stromquelle mit realer Spannungsquelle ersetzt -
Maschen definieren: In diesem Beispiel können 2 Maschen eingezeichnet werden wie in der folgenden Abbildung ersichtlich
Theoretisch könnte noch ein dritter Maschenstrom eingezeichnet werden wie in dieser Abbildung gezeigt:
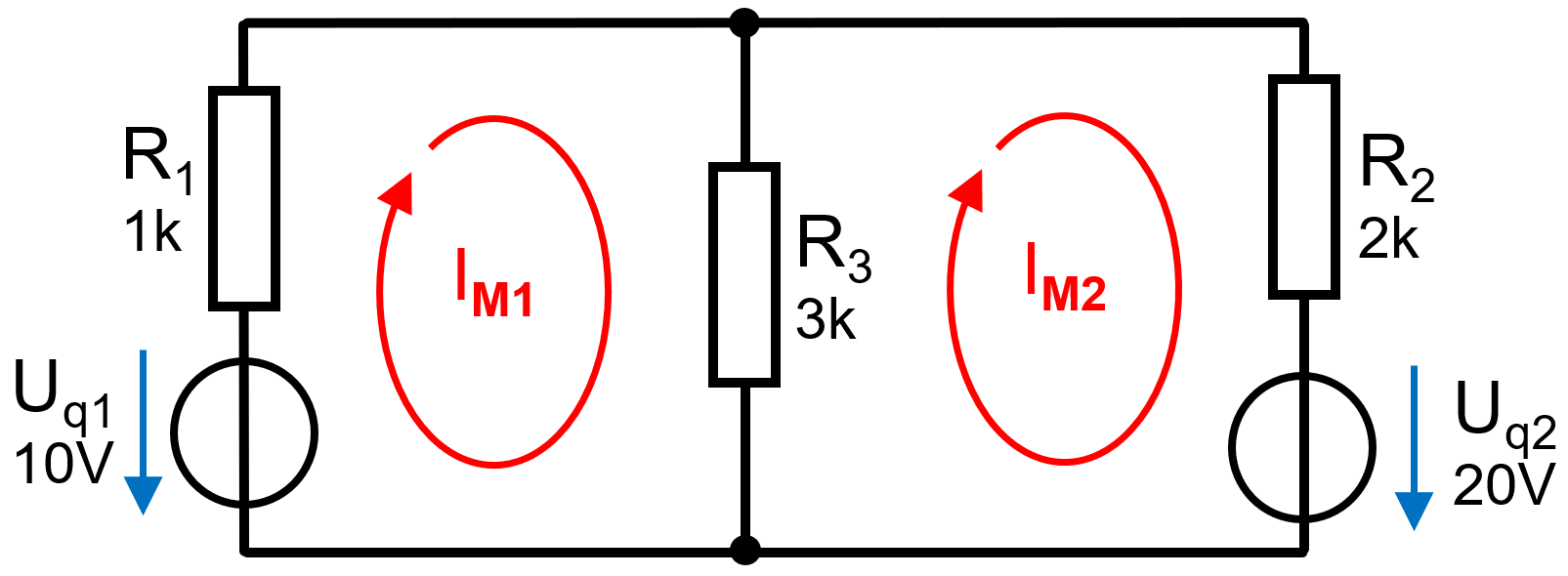
Maschenströme inkl. Richtung eingezeichnet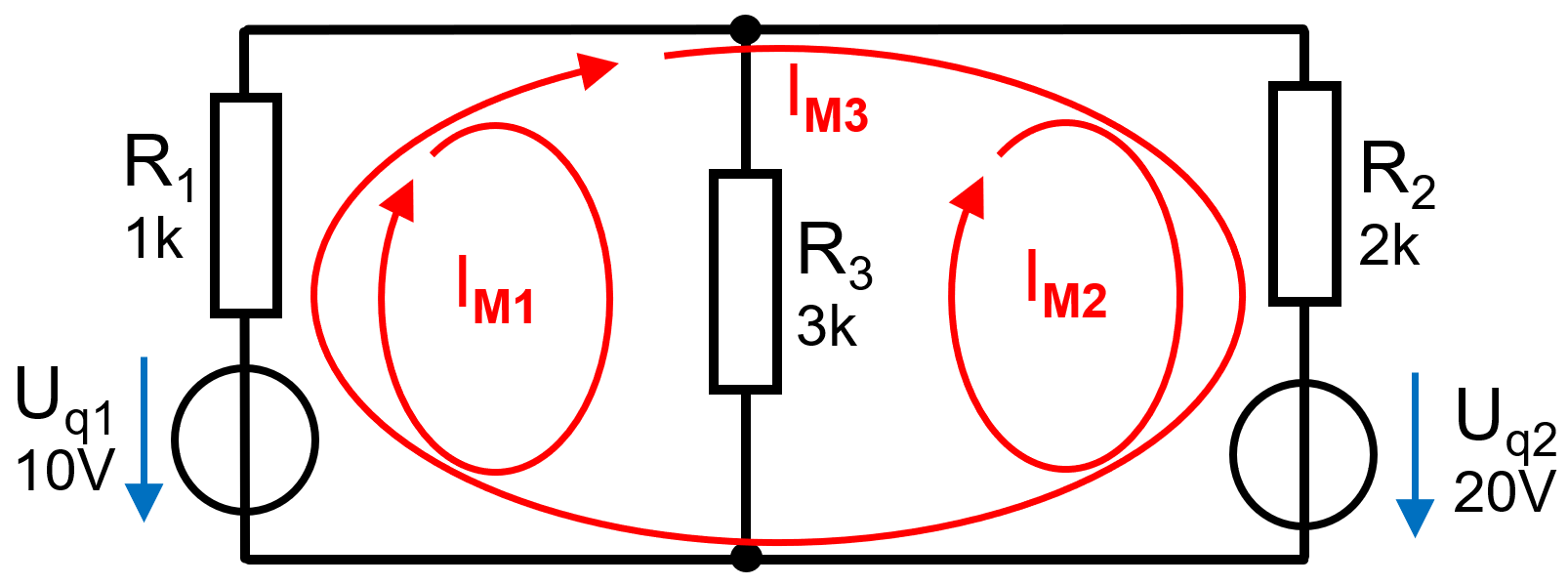
Zuviele Maschenströme inkl. Richtung eingezeichnetDer dritte Maschenstrom wäre grundsätzlich korrekt, ist jedoch aufgrund der Gleichungen nicht notwendig. Sie wird und darf nicht mehr als Gleichung verwendet werden, da der Maschenstrom IM3 entweder durch einen Zweig fließt, durch diesen IM1 oder IM2 fließt. IM3würde sozusagen die anderen beiden Maschenströme überlagern. Dies würde später in der Rechnung ein falsches Ergebnis liefern, da die Zweigströme einzigartig sein müssen und an gewissen Stellen ausschließlich durch Zweige fließen müssen.
-
Aufstellen der Maschengleichungen:
Die Maschengleichungen lauten:
I: \( R_1 I_{M1} + R_3 I_{M1} - R_3 I_{M2} - U_{q1}= 0 \)
II: \( R_2 I_{M2} + U_{q2} + R_3 I_{M2} - R_3 I_{M1} = 0 \)
Es ist erkennbar, dass obige 2 Gleichungen, 2 Unbekannte beinhalten. Somit handelt es sich um ein vollständig bestimmtes Gleichungssystem mit einer eindeutigen Lösung.
-
Gleichungen nach Maschenströmen auflösen:
Es wird die erste Gleichung nach dem Strom \(I_{M2}\) umgeformt
I: \( I_{M2} = \frac{R_1 I_{M1} + R_3 I_{M1}}{R_3} - \frac{U_{q1}}{R_3} \)
in die zweite Maschengleichung eingesetzt ergibt sich:
\( R_2\frac{R_1 I_{M1} + R_3 I_{M1}}{R_3} - R_2 \frac{U_{q1}}{R_3} + U_{q2} + R_1 I_{M1} + R_3 I_{M1} - U_{q1} - R_3 I_{M1} = 0\)
auf \(I_{M1} \) umgeformt ergibt:
\( R_2\frac{R_1 I_{M1} + R_3 I_{M1}}{R_3} + R_1 I_{M1} = R_2 \frac{U_{q1}}{R_3} - U_{q2} + U_{q1}\)
\( I_{M1} = \frac{R_2 \frac{U_{q1}}{R_3} - U_{q2} + U_{q1}}{ \frac{R_2 R_1}{R_3} + R_2 + R_1 } \)
Der Doppelbruch stört im Ergebnis, darum wird mit \(R_3\) ober- und unterhalb des Bruchstriches multipliziert.
\( I_{M1} = \frac{U_{q1} R_2 - U_{q2} R_3 + U_{q1} R_3}{R_2 R_1 + R_2 R_3 + R_1 R_3} \)
mit eingesetzten Werten ergibt sich:
\( I_{M1} = \frac{10V \cdot 2000\Omega - 20V \cdot 3000\Omega + 10V \cdot 3000\Omega}{2000\Omega \cdot 1000\Omega+ 2000\Omega \cdot 3000\Omega + 1000\Omega \cdot 3000\Omega} = -0,909mA \)
nun kann der zweite Maschenstrom berechnet werden
\( I_{M2} = \frac{1000\Omega \cdot (-0,909mA) + 3000\Omega \cdot (-0,909mA)}{3000\Omega} - \frac{10V}{3000\Omega} = -4,545mA \)
die negativen Ergebnisse bei den Maschenströmen zeigt uns, dass sie in die falsche Richtung angenommen wurden. Sie fließen also nicht im Uhrzeigersinn, sondern dagegen.
-
Gesuchte Größen berechnen:
Vorweg müssen die Ströme und Spannungen bei den einzelnen Widerständen eingezeichnet werden. Es bietet sich an, Strom und Spannung bei den Widerständen in die gleiche Richtung zeigen zu lassen (Verbraucherzählpfeilsystem) und bei den Quellen in unterschiedliche Richtugnen zeigen zu lassen (Erzeugerzählpfeilsystem)
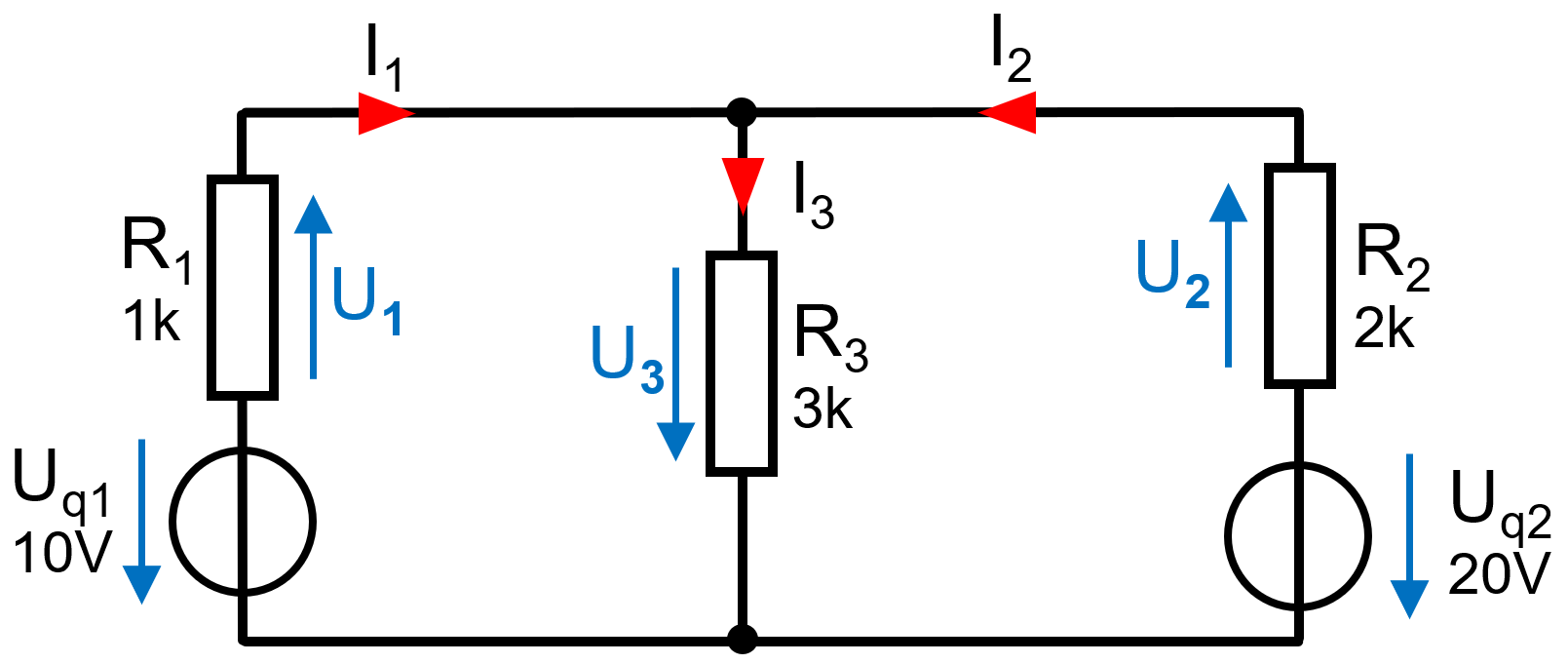
Netzwerk mit eingezeichneten Ströme und SpannungenEs ist erkennbar, dass im linken Zweig beim eingezeichneten Strom I1 ausschließlich der Maschenstrom IM1 fließt. Somit kann I1 berechnet werden mit:
\( I_{1} = I_{M1} = -0,909mA \)
ähnliches gilt für den rechten Zweig mit dem Unterschied, dass der Strom I2 in die entgegengesetzte Richtung wie der Maschenstrom IM2 eingezeichnet ist. Somit gilt
\( I_{2} = -I_{M2} = 4,545mA \)
Beim mittleren Zweig (Strom I3) ist erkennbar, dass er sowohl vom Maschenstrom IM1 als auch von IM2 durchflossen wird. Da I3 nach unten zeigend angenommen wurde und IM1 ebenfalls nach unten zeigt ist dieser Wert positiv einzusetzen. IM2 fließt im mittleren Zweig nach oben und wird daher negativ in der folgenden Rechnung verwendet:
\( I_{3} = I_{M1} - I_{M2} = -0,909mA - (-4,545mA) = 3,636mA \)
Die Spannungen an den Widerständen können nun mit dem Ohm'schen Gesetz berechnet werden.
\( U_{1} = I_{1} R_1 = -0,909mA \cdot 1000\Omega = -0,909V\)
\( U_{2} = I_{2} R_2 = 4,545mA \cdot 2000\Omega = 9,091V\)
\( U_{3} = I_{3} R_3 = 3,636mA \cdot 3000\Omega = 10,91V\)
Nochmals der Hinweis bzgl. des Vorzeichens bei U1. Entweder es wird im Netzwerk die Richtung des Stromes I1 geändert und erhält ein positives Ergebnis, oder man behält die Richtung des Stromes und der Spannung bei und belässt das negative Vorzeichen im Ergebnis.
Übungs-Beispiele
1. Übungsbeispiel
Gegeben ist folgendes Beispiel
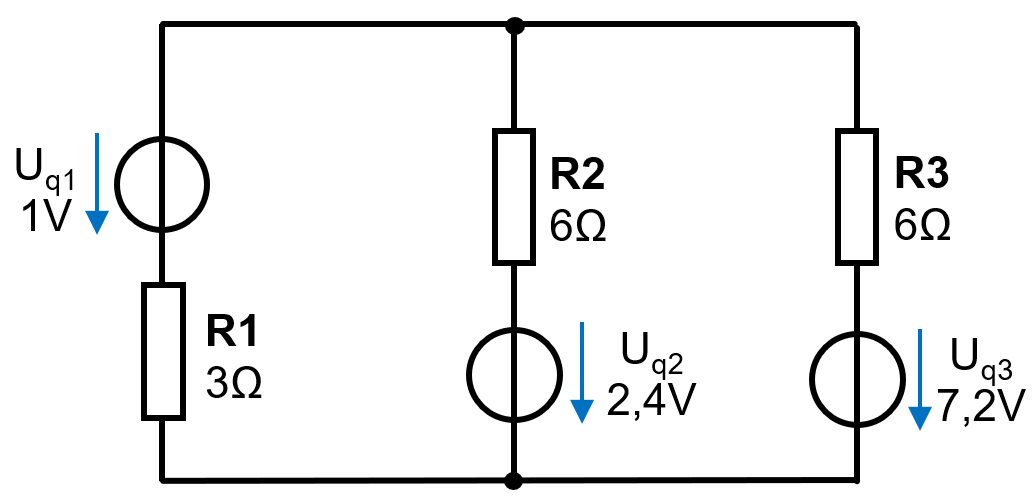
Angabe
2. Übungsbeispiel
Gegeben ist folgendes Beispiel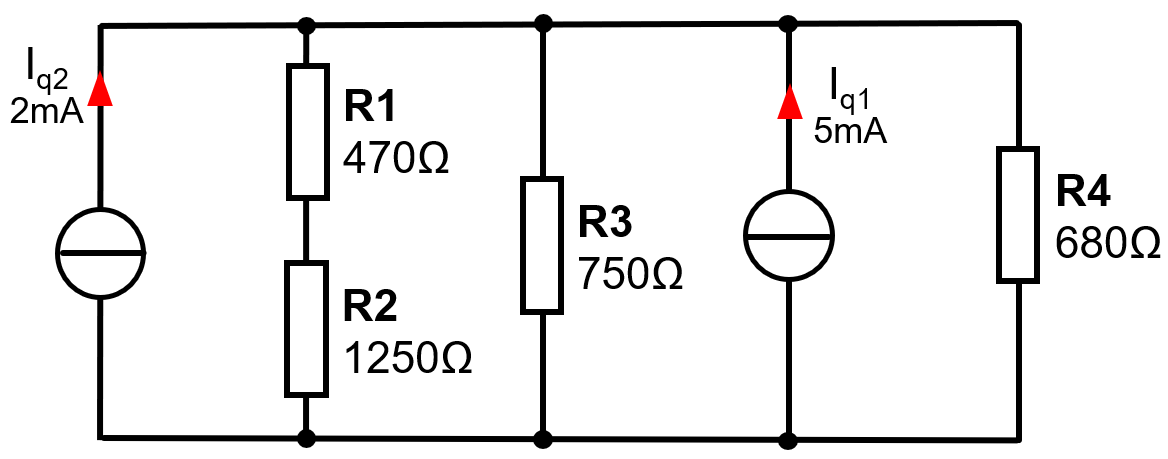
Angabe
Lösung
- Umwandlung in Spannungsquellen: Da ausschließlich Spannungsquellen vorkommen kann dieser Punkt übersprungen werden.
-
Maschen definieren: 2 Maschen können wie in der folgenden Abbildung ersichtlich eingezeichnet werden. In jedem Zweig wirkt zumindest ein Maschenstrom.
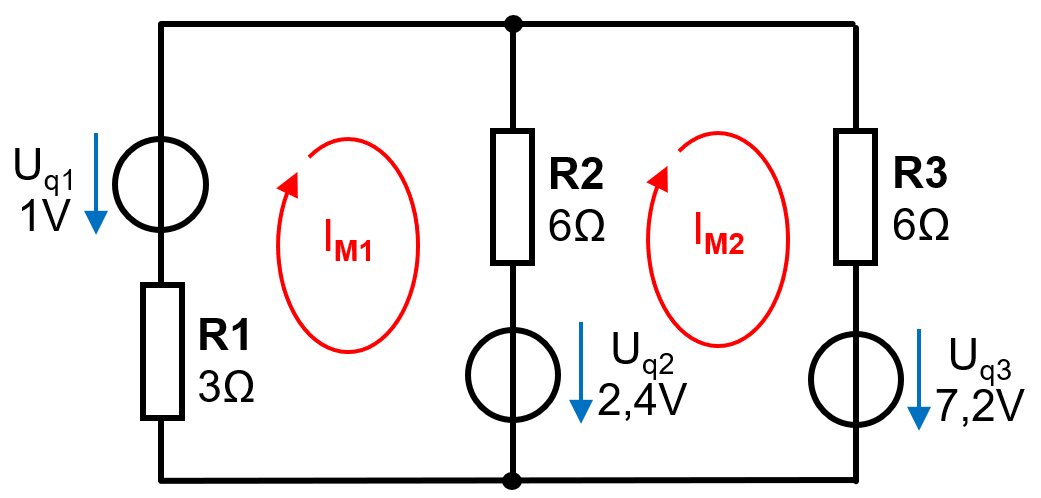
Netzwerk mit eingezeichneten Maschenströmen -
Aufstellen der Maschengleichungen: Die Gleichungen lauten:
I: \( R_1 I_{M1} - U_{q1} + R_2 I_{M1} - R_2 I_{M2} + U_{q2}= 0 \)
II: \( R_3 I_{M2} + U_{q3} - U_{q2} + R_2 I_{M2} - R_2 I_{M1} = 0 \)
-
Gleichungen nach Maschenströmen auflösen: Die erste Gleichung wird auf IM2 umgeformt.
\( I_{M2} = \frac{U_{q2}}{R_2} + I_{M1} - \frac{U_{q1}}{R_2} + \frac{R_1 I_{M1}}{R_2} \)
eingesetzt in die zweite Maschengleichung und nach IM1 ergibt
\( \frac{R_3 U_{q2}}{R_2} + R_3 I_{M1} - \frac{R_3 U_{q1}}{R_2} + \frac{R_3 R_1 I_{M1}}{R_2} + U_{q3} - U_{q2} + U_{q2} + R_2 I_{M1} - U_{q1} + R_1 I_{M1} - R_2 I_{M1} = 0 \)
\( I_{M1} = \frac{-\frac{R_3 U_{q2}}{R_2} + \frac{R_3 U_{q1}}{R_2} + U_{q1} - U_{q3}} {R_3 + \frac{R_3 R_1}{R_2} + R_1} \)
\( I_{M1} = -0,633A \)
für IM2 ergibt sich
\( I_{M2} = -0,717 \)
-
Gesuchte Größen berechnen: Es werden zuerst die Zweigströme wie im oberen Beispiel beschrieben berechnet. Sie sind in der folgenden Abbildung eingezeichnet.
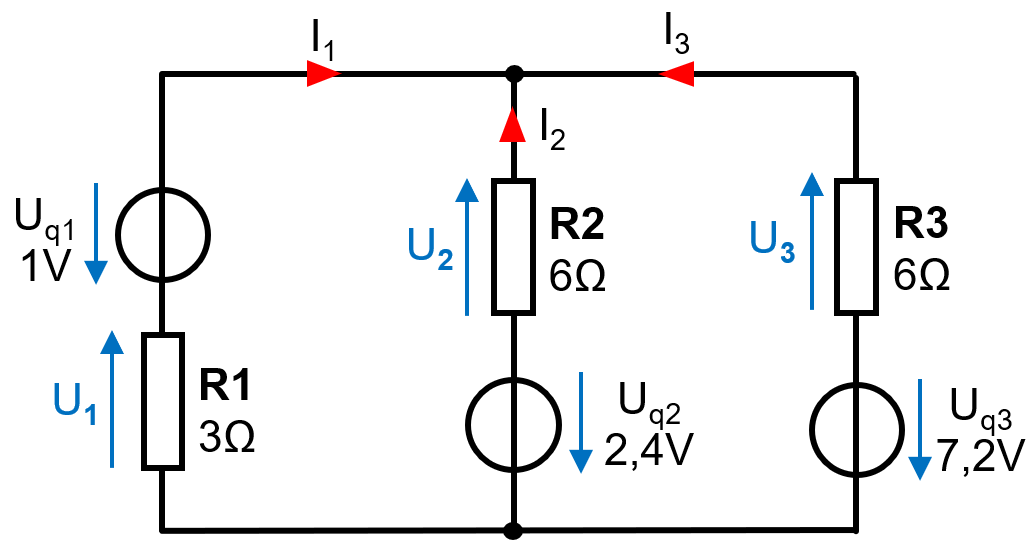
Im Netzwerk eingezeichnete Zweigströme und Spannungen bei den Widerständen\( I_1 = I_{M1} = -0,633 \)
\( I_2 = -I_{M1} + I_{M2} = -0,083 \)
\( I_3 = -I_{M2} = 0,717 \)
Nun werden noch die Spannungen an den Widerständen mit dem ohm'schen Gesetz berechnet.
\( U_1 = I_1 R_1 = -1,9V \)
\( U_2 = I_2 R_2 = -0,5V \)
\( U_3 = I_3 R_3 = 4,3V \)